Predicción del riesgo de cáncer utilizando el aprendizaje automático del estilo de vida y los datos genéticos

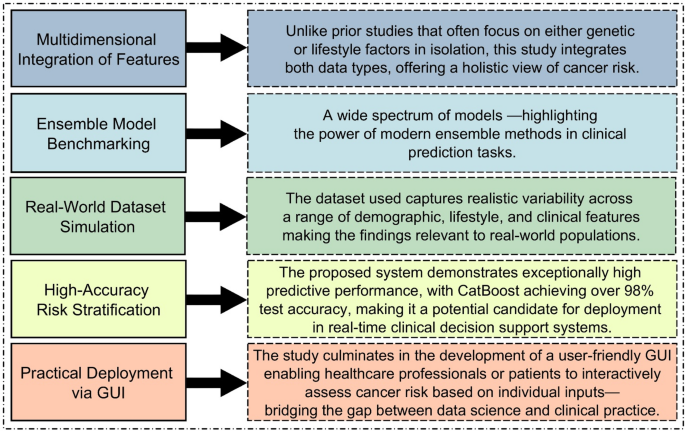
Presentación del conjunto de datos

El conjunto de datos utilizado en este estudio consistió en 1,200 registros de pacientes, recopilados en archivos de Excel con columnas etiquetadas estructuradas de varios datos clínicos y de estilo de vida, y en este estudio utilizamos un subconjunto de conjuntos de datos de predicción del cáncer publicados (1,500 de 1,500 muestras) compartidos bajo el riesgo de cáncer y los días de comunicación de cáncer. El conjunto de datos incluye un total de nueve características además de las variables objetivo utilizadas para la predicción. Una descripción detallada de todas las características y sus tipos se da en la Tabla 2.

Las variables de diagnóstico son los objetivos para las predicciones para este estudio. Promueve la clasificación del paciente de acuerdo con el estado de diagnóstico de cáncer. El conjunto de datos se distribuye de manera justa entre las características y las clases objetivo, facilitando un procedimiento de entrenamiento imparcial para el modelo ML.

Un gráfico de distribución de frecuencia llamado histogramas creó edad, IMC, actividad física y ingesta de alcohol para visualizar la distribución de variables continuas dentro del conjunto de datos. Estos factores representan aspectos importantes de la salud y el estilo de vida individuales que pueden estar relacionados con el riesgo de cáncer. La distribución de edad de las subtramas es principalmente uniforme en el rango de 20-80, con un ligero aumento en la frecuencia de los adultos mayores. La distribución del IMC de las subtramas Figura 2 (b) se distribuye uniformemente entre 15 y 40, lo que significa una población de pacientes heterogéneas en términos de composición corporal. Actividad física La Figura 2 (c) de la subplotación muestra la variación entre la población y se observa en todos los niveles entre 0 y 10 horas por semana. El consumo de alcohol representado en la subplotación se muestra en la Figura 2 (d) con una distribución uniforme que varía de 0 a 5 unidades, sin agrupaciones significativas. El histograma muestra que el conjunto de datos exhibe una variabilidad auténtica y es equilibrado y esencial para construir un modelo ML robusto y generalizable, como se ve en la Figura 2.

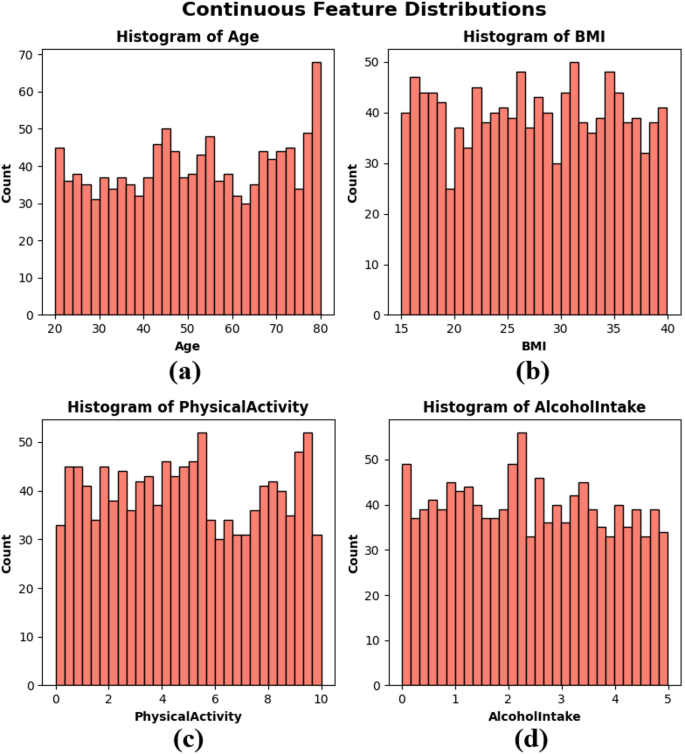
Histogramas de características continuas – (a) edad, (b) IMC, (c) actividad física y (d) ingesta de alcohol.

Se crearon diagramas de caja para mostrar la distribución, las tendencias centrales y los posibles valores atípicos de las variables continuas dentro del conjunto de datos. La Figura 3 (a) muestra la distribución de edad para la mediana de edad de aproximadamente 50 años, el rango intercuartil (IQR) de aproximadamente 35-65 y la ausencia de atípicos extremos. La funcionalidad del IMC de la subtrama Figura 3 (b) muestra una distribución estrecha y equilibrada con un valor medio de alrededor de 27, con un IQR estrecho que muestra valores de composición corporal similares entre las muestras. Actividad física La Figura 3 (c) en la trama secundaria varía de 0 a 10 horas por semana con una mediana de casi 5, lo que refleja una distribución equilibrada de los niveles de actividad física del paciente. Finalmente, el consumo de alcohol de la trama subplotta La Figura 3 (d) también muestra una amplia distribución de 0-5 unidades por semana, con una mediana ligeramente por encima de 2 unidades. Los gráficos de caja, como se muestra en la Figura 3, muestra que el conjunto de datos no tiene una gran asimetría o valores atípicos extremos para características continuas, lo que respalda el ajuste del modelo de entrenamiento en ML.

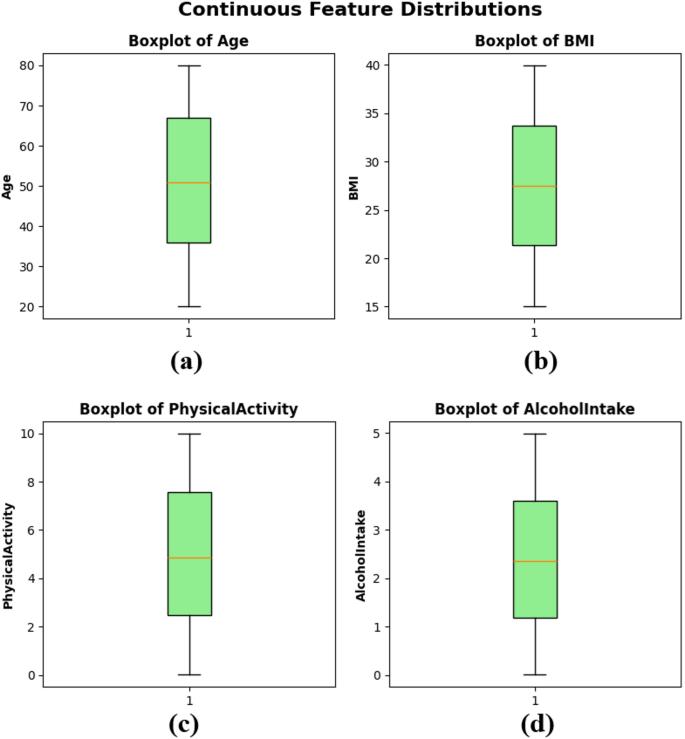
Rapas de caja de características continuas – (a) edad, (b) IMC, (c) actividad física y (d) ingesta de alcohol.

Se crearon gráficos de recuento para evaluar la distribución de datos categóricos y binarios, particularmente con respecto al género, el tabaquismo, el cáncer y el entorno genético. La Figura 4 muestra que la distribución de género de las subtramas está aproximadamente equilibrada entre los hombres (0) y las mujeres (1) e implica una representación imparcial del género general. La Figura 4 (b) muestra que la mayoría de los pacientes no son fumadores, lo que puede indicar tendencias de estilo de vida en la población. En la Figura 4 (c) de la barra lateral, la mayoría de los pacientes no muestran antecedentes personales de cáncer, pero aún así se ha diagnosticado previamente una proporción prominente. Factores de riesgo genético para subtramas La Figura 4 (d) se clasifica en niveles bajos (0), medio (1) y altos (2). La mayoría de los pacientes se clasifican como de bajo riesgo, mientras que un pequeño número se considera de alto riesgo. Estas gráficas muestran las propiedades equilibradas y la variabilidad auténtica del conjunto de datos, lo que confirma que el modelo está entrenado en una muestra representativa, como se muestra en la Figura 4.

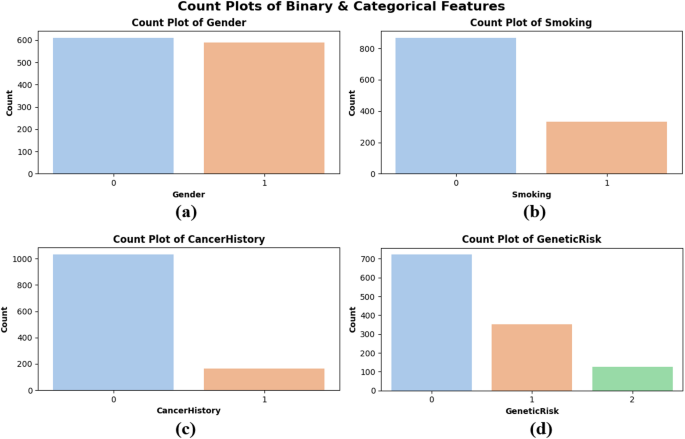
Cuente gráficos de características binarias y categóricas – (a) género, (b) fumar, (c) historial del cáncer y (d) riesgo genético.

Las correlaciones de matriz proporcionan lecturas estadísticas para cada relación lineal entre la función del conjunto de datos y el objetivo (diagnóstico). Como se puede ver en la Figura 5, Cancerhistory tiene la mayor correlación con el objetivo, con un valor de correlación de 0.41. Esto significa una relación lineal leve. Esto significa que los pacientes que han tenido cáncer en el pasado son más relevantes clínicamente y tienen más probabilidades de tener cáncer en el futuro. Otras características que están altamente correlacionadas con las variables objetivo incluyen género (0.28), riesgo genético (0.27) y fumar (0.26). Si bien la mayoría de los pares de características exhiben correlaciones débiles o insignificantes, como el IMC, la inducibilidad de genes, la edad y la actividad física, esta diversidad indica multidimensionalidad del conjunto de datos y justifica el uso de modelos no lineales para capturar interacciones complejas. Las observaciones de correlación anteriores en la Figura 5 están justificadas para una mayor influencia en el modelado predictivo, confirmando así la importancia de las características seleccionadas.

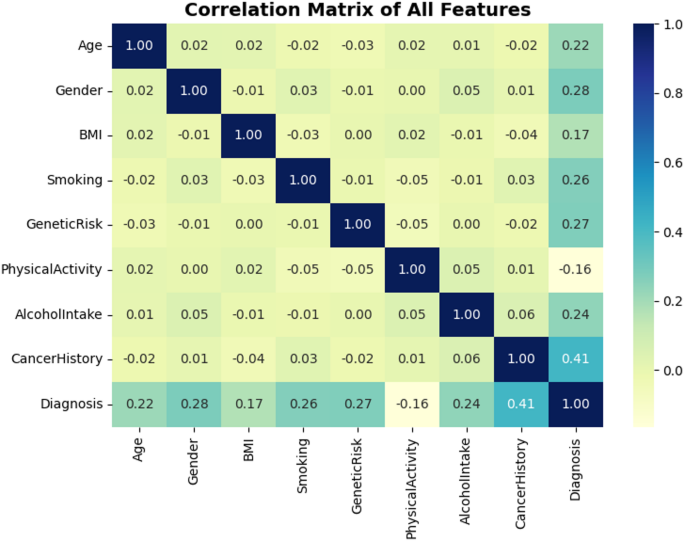
Una matriz de correlación para todas las funciones, incluido el diagnóstico.

Descripción general del flujo de trabajo

La metodología de este estudio sigue un enfoque estructurado y basado en datos para desarrollar sistemas precisos de predicción del cáncer utilizando ML, como se muestra en la Figura 6. El proceso comienza con la carga de un conjunto de datos que contiene diversas características del paciente, como edad, sexo, IMC, estado de tabaquismo, riesgo genético, actividad física, consumo de alcohol e historia personal de cáncer. Una vez cargado, el conjunto de datos sufre una investigación exhaustiva para comprender su estructura e integridad. Se examina la información básica como la forma, las filas de muestra y los valores faltantes, seguido de un resumen estadístico que proporciona información sobre la distribución de cada característica. Para mejorar esta comprensión, EDA se realiza a través de visualizaciones como histogramas, gráficos de cajas y parcelas de recuento para ayudar a identificar patrones y anomalías. También se genera una matriz de correlación para detectar relaciones entre variables numéricas.

Después de la investigación, si el conjunto de datos se divide en funciones de entrada y etiquetas de destino, se realiza el preprocesamiento de datos. Las características continuas se estandarizan utilizando StandardScaler para garantizar una escala uniforme entre los modelos. El núcleo de la metodología está en el entrenamiento de regresión logística (LR), árbol de decisión (DT), RF, Gradient Boost (GB), Support Vector Machines (SVM), K-Nearest NeighboBors (K-Nn), Catboost, BowCece Bounding (XGBOOST) y Máquina de soporte de gradiente de luz (Lightgifting CossgbMid), CatBoosting, Extramost, K-Nn), K-Nnn) Máquinas (SVMS), Máquinas de vectores de soporte (SVMS), Máquinas de vectores de soporte (SVM) y Máquinas de vectores de soporte (SVM). Esto garantiza una evaluación equilibrada y robusta al evaluar la precisión de cada modelo en diferentes segmentos de datos. El modelo con la más alta precisión promedio de validación cruzada se elige como el mejor modelo de rendimiento.

Para verificar aún más el rendimiento del modelo, se aplican las divisiones de prueba de trenes y todos los modelos se evalúan con datos de prueba invisibles. Se calculan las métricas clave como la precisión, la precisión, el retiro y la puntuación F1 para cada modelo, y la matriz de confusión se traza para visualizar el rendimiento de la clasificación. Todos los resultados de la evaluación se guardan como archivos CSV para la reproducibilidad y el soporte de informes. Finalmente, se desarrolla una GUI utilizando Tkinter, lo que permite a los usuarios ingresar información del paciente y recibir predicciones instantáneas del modelo capacitado. Este flujo de trabajo de extremo a extremo garantiza que el sistema no solo sea preciso y confiable, sino también prácticamente accesible y fácil de usar.

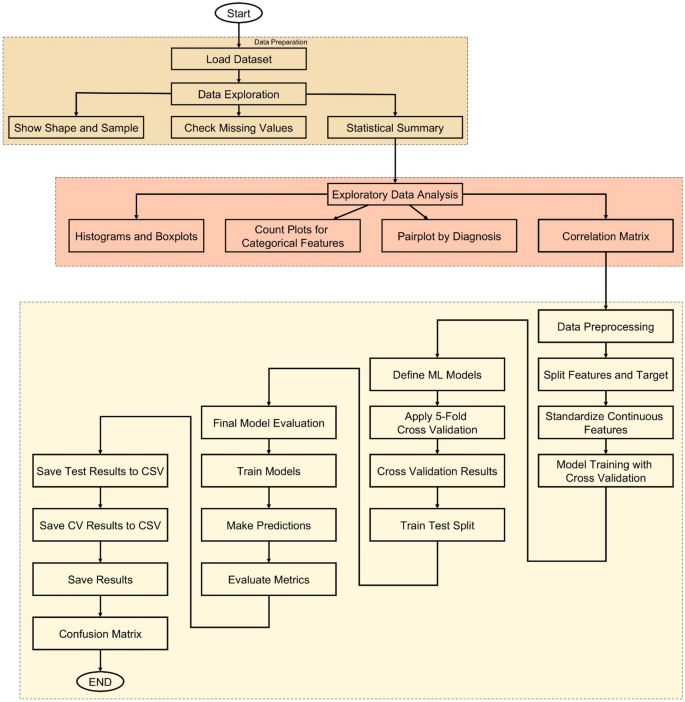
Flujo de trabajo de extremo a extremo para sistemas de predicción del cáncer que incorporan exploración de datos, capacitación modelo, evaluación y implementación de GUI.

Métricas de calificación

Se emplearon varias métricas de clasificación general para verificar la efectividad del modelo ML desarrollado. Estas medidas ayudan a tener una visión general completa de la eficiencia de cada modelo al aislar pacientes en pacientes con o sin enfermedad, un aspecto muy importante de todas las tareas de predicción relacionadas con la salud.

Uno de los indicadores es la precisión definida, en particular, como el porcentaje de predicciones correctamente clasificadas (tanto negativas como positivas) en todas las predicciones realizadas. Esto proporciona un sentido general de precisión del modelo, como se muestra en la ecuación. (1). Sin embargo, la precisión por sí sola puede no ser suficiente para conjuntos de datos médicos, especialmente cuando los costos de FNS o FPS son altos.

La precisión y el recuerdo también se evaluaron para obtener información más profunda. La precisión mide el porcentaje de casos positivos verdaderos (TP) entre todas las predicciones positivas. Esto es importante para minimizar las falsas alarmas y evitar preocupaciones innecesarias y procedimientos de seguimiento para individuos sanos. (2). Por otro lado, también conocido como sensibilidad, se centra en la capacidad del modelo para identificar correctamente los casos de cáncer reales, asegurando que no se detecten la mayor cantidad de casos positivos como sea posible. Esto se calcula como se explica en la ecuación. (3). Debido a que generalmente hay una compensación entre precisión y retiro, este estudio utilizó las puntuaciones de F1 para usar un puntaje de rendimiento único que equilibra ambos. Esto es útil cuando recuerda el promedio de armónicos con precisión y cuando hay una ligera clase de desequilibrio, o cuando se trata de FPS y FNS. Matemáticamente, la puntuación F1 se define por una ecuación. (4).

Además de estas métricas escalar, se creó una matriz de confusión para cada modelo, lo que indica la cantidad de TP, verdadero negativo (TNS), FPS y FNS. Esto ha alentado una comprensión clara del rendimiento del modelo en diferentes tipos de predicción.

Cada modelo se evaluó primero utilizando un enfoque de validación cruzada de 5x en capas, manteniendo la distribución de clases dentro de cada pliegue. Esto proporcionó una sólida evaluación de las capacidades de generalización del modelo. Luego se evaluó el modelo con un conjunto claro de prueba de retención del 20%, y se calcularon métricas idénticas para medir los efectos predictivos reales.