Learning the fitness dynamics of pathogens from phylogenies

Sequence data

For each pathogen, we compiled a dataset to investigate the changes in the population composition. For SARS-CoV-2 and H3N2, we extracted the datasets from the publicly available NextStrain37 time-resolved phylogenies, accessed on 14 April 2023. These datasets are sub-samples from all publicly available sequences in GISAID, to represent the diversity as much as possible (we used the ‘all-time’ dataset for SARS-CoV-2 and the ‘12 y’ one for H3N2). In all, we have 3,129 whole-genome SARS-CoV-2 sequences sampled from 26 December 2019 to 3 April 2023, and 1,476 H3N2 HA sequences from 1 January 2005 to 3 April 2023 (Supplementary Tables 10 and 11). For B. pertussis, we used 1,248 sequences from 1953 to 2022, collected by the National Reference Center for Whooping Cough and Other Bordetella Infections in France (Supplementary Table 12). This dataset is composed of 1,023 previously published sequences3,38,39,40,41 and 225 newly sequenced isolates. The new isolates have been sequenced with the same methods as previously described3. This dataset is representative of the B. pertussis diversity in France as the National Reference Center receives isolates from 42 sentinel hospitals throughout France. For M. tuberculosis, we used 997 previously published sequences, isolated in 2008–2010 in Samara, Russia20. This dataset is also representative of M. tuberculosis sequence diversity at that location as isolates were prospectively collected from individual patients living in the region and representative of the entire population (Supplementary Table 13).

Multi-sequence alignment for each pathogen

We compiled alignments of all sequences. For SARS-CoV-2, we used the precomputed multi-sequence alignment provided by GISAID. For H3N2, we aligned all HA sequences using MAFFT42 (v.7.309) with default settings. We then manually checked that the alignment did not have any frameshift and had minimal gaps. For B. pertussis and M. tuberculosis, we worked from raw reads with a previously described protocol3. Reads were trimmed using Cutadapt43 (v.3.4) and quality was checked with FastQC44 (v0.11.9). Using BWA-MEM45 (v0.7.17), reads were mapped against the complete Tohama I reference genome (accession number in RefSeq: NC_002929) or the complete H37Rv reference genome (accession number in RefSeq: NC_000962.3). Using GATK46 (v.4.2.0.0), we kept variants that were present in at least 75% of reads, with a Phred quality score higher than 30, a minimum read depth of 5, a minimum mapping quality of 20 and a string odd ratio of less than 3. We masked all positions that were covered by less than five reads. Furthermore, we filtered out regions that are notoriously difficult to map and/or sequence, similarly to previous studies3,47. Namely, for B. pertussis we filtered out repeated regions (IS481, IS1002 and IS1663)35 and phage regions using PHASTER48; for M. tuberculosis, we filtered out the functional categories ‘PE/PPE’ and ‘insertion sequences and phages’47. For B. pertussis, we also checked for recombination in our alignment using Gubbins49 (v.3.3.0). As a result, we obtained an alignment of 4,701 SNPs for B. pertussis and 30,533 SNPs for M. tuberculosis.

Reconstruction of time-resolved phylogenies

For each pathogen, we obtained time-resolved phylogenies. For SARS-CoV-2 and H3N2, we used the NextStrain trees, accessed on 14 April 2023 (ref. 37). For B. pertussis and M. tuberculosis, we reconstructed the timed phylogenies specifically for this study using the SNP-based alignments. We first built maximum-likelihood trees using IQ-tree50 (v.2.1.0) using a GTR + F + G substitution model. To assess the branch support, we used the ultrafast bootstrap approximation provided in IQ-tree, performing 1,000 replicates for each dataset with the bnni option to reduce the risk of overestimating the branch support51.

For B. pertussis, the time tree was reconstructed using BEAST v.1.10.452, under a GTR substitution model18 accounting for the number of constant sites, a relaxed lognormal clock model53 and a skygrid population size model54. Three independent Markov chains were run for 150,000,000 generations each, with parameter values sampled every 10,000 generations. Runs were optimized using the GPU BEAGLE library55 (v.4.0.0). Chains were manually checked for convergence (effective sample size values > 200) using the Tracer software56 (v.1.7.2). We manually removed a 10% burn-in.

For M. tuberculosis, because all sequences were isolated in 2008–2010, we could not infer a clock rate, but instead, we used a previously estimated clock rate57 of 4.6 × 10−8 mutations per site per year. We used the software BactDating58 (v.1.1) to perform a Bayesian reconstruction of the time tree. We used a fixed mean substitution rate, a relaxed clock rate and a constant effective population size. We ran the chain for 10,000,000 iterations and checked for convergence (effective sample size values > 200).

Index definition

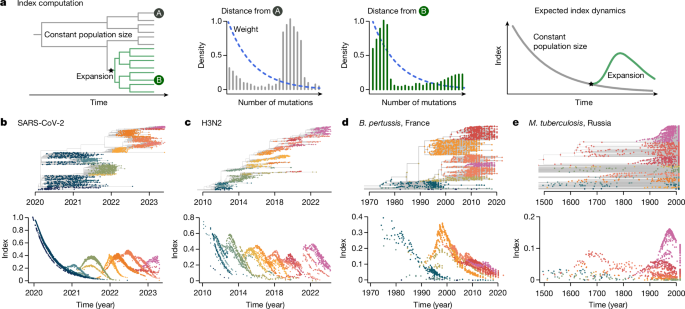
We developed an analytical approach that summarizes the changes in population composition in phylogenetic trees at every time point. Our approach builds on a genetic distance-based index, the timed haplotype density16, that measures the epidemic success of individual sequences in a dataset. This measure is based on the expectation that sequences sampled from an emerging, fitter lineage will be phylogenetically closer than the rest of the population at that time, as they will all share the same recent ancestor. We extend this method to track population changes in phylogenetic trees through time.

We define the index of each isolate i in its population at time t as:

Where Di(d,t) the distance distribution—in number of mutations or evolutionary time (branch length)—from isolate i to the rest of the population (internal and terminal nodes) at time t (Fig. 1) and bd is the kernel setting the weight of each distance d. b is the bandwidth, b ∈(0, 1), which is a parameter to set, linked to the timescale. We compute this index on each node in a tree (internal and terminal).

The weight allows us to track lineage emergence dynamically, focusing on short distances between nodes (containing information about recent population dynamics) rather than long distances (containing information about past evolution). The kernel is governed by the bandwidth b, which is a parameter to set. As b is dimensionless, it is hard to set. Instead, we use the notion of timescale 50 to choose it: the time to the most recent common ancestor (TMRCA) was chosen such that pairs of isolates with shorter TMRCAs account for 50% of the kernel density16. This timescale is tailored to the specific pathogen studied and its choice will depend on the molecular signal, as well as the transmission rate. Here we used timescales ranging from 1.8 months (SARS-CoV-2, RNA virus) to 30 years (M. tuberculosis, a bacterium) (Supplementary Table 1).

Our approach provides a quantitative index value for each node (internal and terminal) in the tree, independently of any lineage classification providing an advantage over other methods that rely on lineage classification. This enables us to agnostically summarize the changes in population composition in phylogenetic trees at every time point.

Our definition is nearly the same as the one used in a previous study16, with two critical differences: instead of computing the index by summing on each isolate in the population we now sum over the pairwise distance distribution, and we consider the collection time of each sequence to only compute the distance from i to the rest of the population that is circulating at that time.

This index is similar to the local branching index10, which is defined as the total surrounding tree length exponentially discounted with increasing distance from isolate i. In our case, rather than considering the tree length, we compute the distance between nodes.

This index definition enables us to write an expectation of the index dynamics over time, as theoretical pairwise distance distributions can be approximated for different populations. In practice, to compute the index of each node in a phylogenetic tree, we sum over the distance to all nodes in the population, rather than the distance distribution (see ‘Index computation on time tree with sequences sampled through time’ section).

Linking the index dynamics to population history

The pairwise distance distribution Di(d,t) or more generally D(d,t), can be seen as the probability, \({P}_{c}(s=\frac{d}{\mu l},t)\), for any pair of sequences sampled at time t, to coalesce some time \(s=\frac{d}{\mu l}\) in the past, with μ being the rate at which the pathogen accumulates mutations per site and per unit of time and l the length of its genome.

Therefore, at any time point, writing the probability of coalescing in the past enables us to compute the index in the population. We can update equation (1):

We note that at time t, the maximum number of mutations accumulated is equal to μlt. For simplicity, we assume a linear accumulation of mutations through time in all the analytical expressions, although one could consider that mutations accumulate randomly given a Poisson distribution with rate 1/(μlt).

This probability \({P}_{c}(s=\frac{d}{\mu l},t)\) is closely linked to the effective population size. In Supplementary Fig. 13, we show conceptually how, for different effective population sizes, the probability of coalescing changes, and how it affects the index dynamics. Formal derivations are presented in the Supplementary Information.

Index computation on time tree with sequences sampled through time

We use equation (1) to compute the index of each node (internal or terminal) in a timed phylogenetic tree. To do this, for each node i, we compute its distance to all the other nodes present in the tree at that time (see Supplementary Fig. 14 for notations). All the nodes that fall in the time interval (ti – twind; ti + twind) are considered to be circulating at the same time as i; with ti being the collection time of node i and twind the predefined time window width that is tailored to each pathogen. We also consider extant branches in the computation, as they are evidence of past circulation.

For computation efficiency, similarly to the previously published study16, we then compute:

Where nodes indicates the set of all nodes in the tree, and I() is the indicator function.

This computation is efficient as it only requires the precomputation of the indicator function, the precomputation of the distance matrix and a matrix multiplication.

For the pathogens presented in our study we used the following parameters. SARS-CoV-2: a timescale of 0.15 years, and a window of time twind = 15 days. H3N2: a timescale of 0.4 years, and a window of time twind = 0.25 years. B. pertussis: a timescale of 2 years, and a window of time twind = 1 years. M. tuberculosis: a timescale of 30 years, and a window of time twind = 15 years.

We illustrate the impact of the timescale on the index dynamics in Extended Data Fig. 8 for the global SARS-CoV-2 tree.

To test the robustness of the index computation for the exact tree topology, we ran a sensitivity analysis on 3,000 trees sampled from the posterior of the BEAST run of B. pertussis. We chose B. pertussis for this analysis because it is the only pathogen for which we have a posterior distribution of trees. We repeatedly computed the index on each tree sampled from the posterior and computed the average index of each tip. Although there is uncertainty in the exact value of the index for each tip, we found that the index dynamics of each lineage remained very consistent across the posterior of trees (Supplementary Fig. 15).

Agnostic detection of lineages

We develop an approach that is able to find the set of lineages in the tree that best explains the index dynamics. To do this, we build an algorithm based on generalized additive models (GAM) that jointly uses the phylogenetic relationships between nodes in the tree and their index.

In this section, for modelling purposes, we define lineages as monophyletic clades formed by one internal node and all its descendants. Here, these lineages can overlap, meaning that some isolates can be included in multiple lineages. We assume the tree to be binary. For a rooted binary tree with n terminal nodes, there are n – 2 internal nodes that are not the root, and therefore n – 2 lineage possibilities—a substantial number. To keep the algorithm tractable, we limit the potential list of lineages to those starting with an internal node that has at least Noff offspring, where Noff is chosen. We note the set of internal nodes to test \(\Pi \). Furthermore, to increase the accuracy of the detection, we take into account only internal nodes that have predefined characteristics. For B. pertussis and M. tuberculosis, as we constructed the bootstrap support of each node (see above), we consider only internal nodes that have a bootstrap support of at least 50% to be the potential start of lineages. This threshold is low, but effectively removes nodes that are not well supported. For SARS-CoV-2 and H3N2, instead of bootstrap support, we consider a minimum number of mutations. We consider only internal nodes that have a least one mutation on the branch directly upstream from them.

The algorithm models the log index through time. We use a log transformation to avoid having to restrict to model to positive values and to make sure the model does not overfit the index peaks.

The log index of each lineage l is modelled using a cubic spline Sl(t, k) with a predefined number of knots k. This allows us to model the log index of each node i, sampled at time ti, given the lineage that it belongs to:

Where β0 is the intercept, L is the total number of lineages, S0(t, k) and Sl(t, k) are penalized cubic regression splines with k knots59. One null spline S0(t, k) is estimated to model the initial population, together with one spline for each of the L lineages. If L = 0, then no Sl(t, k) is estimated. I() is the indicator function: I(i ∈ l) = 1 if i is a member of the lineage l, and 0 otherwise.

In brief, the algorithm runs as follows. We start with a null model M0 that fits the index dynamics with one spline S0(t, k) (that is, an unstructured population with one single index dynamic, L = 0). We store the deviance explained Dev0 by model M0. We then sequentially consider models with increasing complexity ML: we start by first trying models with one lineage, L = 1. We go through the list of internal nodes π that could be the start of a new lineage. When the deviance explained Dev1 by the best model M1 is higher than that of the previous null model Dev0 we keep the lineage (effectively the node from π) that best explains the dynamics. We then continue this procedure for increasing L. For each number L, we go through the list of internal nodes π that could be the start of a new lineage. When the deviance explained DevL by the model ML is higher than that of the previous model DevL–1, we keep the lineage (effectively the node from π) that best explains the dynamics.

The algorithm is implemented in R v.4.1.2, using the package mgcv v.1.8 (ref. 60) to implement the GAM models.

As for any clustering algorithm, choosing the best number of lineages that describe the index dynamics is a challenging question. We took the approach of the elbow plot. We plot the deviances DevL explained by each best model ML, as a function of the number of lineages L. This approach enables us to see how well all the models are performing, and to choose the number L of lineages at which the deviance explained does not increase substantially anymore (Extended Data Fig. 9). From this selected best number of lineages Lbest, we then compute the equivalent set of non-overlapping lineages presented in this paper (Figs. 1–5 and Extended Data Fig. 4). We make sure the minimum number of nodes per non-overlapping lineage is at least Nmin by merging the small lineages to their respective phylogenetically closest lineages.

In simulations, we demonstrate a clear elbow that precisely identifies the optimal number of discrete lineages in the dataset (Supplementary Fig. 16). However, not all pathogens in real-world datasets will give clear elbows. This may be due to insufficient sampling intensity and the presence of lineages with only very small differences in fitness. In practice, increasing the number of distinct lineages will progressively lead to the identification of lineages with increasingly reduced fitness differences, with increasing risks of falsely dividing lineages into subpopulations between which no true differences exist.

For the pathogens presented in our study we found: SARS-CoV-2, 14 lineages; H3N2, 20 lineages; B. pertussis, 8 lineages; and M. tuberculosis, 12 lineages.

To compare the automatic lineages found with phylowave to those previously identified, we compute a contingency matrix C. Let U be the partition of the isolates by phylowave and V the partition based on the literature. Each element Ci,j is the number of isolates in both clusters ui and vj. In Fig. 2, we plot the matrix as a heat map, normalized by column j. We computed the ARI to measure the agreement between partitions, accounting for random clustering21. A value of 1 corresponds to perfect agreement with previously identified lineages, whereas a value of 0 would be expected if clusters were assigned at random.

We illustrate the impact of the timescale on lineage detection in Extended Data Fig. 8 for the global SARS-CoV-2 tree.

Quantifying the fitness of each lineage

We developed a multinomial logistic model that takes into account the birth of lineages to fit the proportion of each lineage through time and quantify their fitness.

The proportion p•, t of sequences at time t from each lineage is computed as the number of nodes (internal and terminal) divided by the total number of nodes (internal and terminal) in the population at that time. This proportion p•, t is modelled by:

Where α• is the vector of the intercept, denoting the initial relative prevalence of each lineage in the population and β• the vector of the relative growth rates of each lineage. We assume that each lineage i has a constant relative growth rate βi in the population, that is, each lineage has a constant relative fitness through time. We compute all the relative growth rates with reference to the oldest lineage.

We use a Laplace prior for the growth rate coefficient (where ~ denotes ‘distributed as’)8:

We take into account lineage birth by only allowing only pi,t, the lineage i proportion in the population at time t, to be non-negative after the MRCA of the lineage. Formally, this is done by parameterizing α• as follows. We divide the lineages into two types, either ancestral or non-ancestral. An ancestral lineage is a lineage that is present at the beginning of the time series considered. The total number of ancestral lineages is noted G. For those lineages, we sample directly their starting proportions with prior:

A non-ancestral lineage is a lineage that appears after some time−for example the Omicron variant. For those lineages, we assume that their starting frequency, at the time of emergence, is a function of the proportion of their parents in the population at that time. Thus we write:

Where j is the parent lineage of lineage i, \({p}_{j,{t}_{{\rm{MRCA}}i}}\) is the proportion of the parent lineage j at the time of emergence \({t}_{{\rm{MRCA}}i}\) of the offspring lineage i and γi is the share of the parent lineage that is becoming the new lineage. We sample γi with a strong prior because we expect that the starting proportion of new lineages should be small:

Finally, we update the parent j proportion as follows:

Although this parameterization is more complex than the previous efforts using a similar model8, it enables us to take into account that lineages appear through time, which makes the model more biologically relevant (for example, by not estimating the proportion of Omicron in the population in 2020). We chose to parameterize the starting proportions of the new lineages as a function of the proportion of their parents so that the model is biologically sound, that is, the starting proportion of a new lineage cannot be greater than the one of its parent, and the starting proportions are constrained by the proportion of the parents. The parameters make the model statistically easier to fit.

We use a multinomial likelihood to fit the count of sequences per lineage through time y•, t:

We further computed the inferred real-time growth rate (that is, the fitness) ri



Source link